CALCULUS Understanding
Its Concepts and Methods
CALCULUS Understanding
Its Concepts and Methods
Inner product, Dot product
The inner product, or
dot product, of two vectors
and
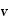is defined
as
where
is the angle between
and
,
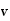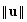and
and
are the lengths of the vectors
and
,
respectively.
The inner product or
dot product of two vectors in
is given algebraically
by
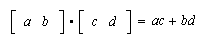
The inner product or
dot product of two vectors in
is given algebraically
by
The inner product is a number, not a vector. If
and
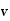are perpendicular, then
.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Copyright © 2006 Darel Hardy, Fred Richman, Carol Walker, Robert Wisner. All rights reserved. Except upon the express prior permission in writing, from the authors, no part of this work may be reproduced, transcribed, stored electronically, or transmitted in any form by any method.